It is well known by now that an internal combustion engine only gives maximum power at a certain range of revolutions and under a certain load, the rest of the time the power delivered is a fraction of the same, corresponding to the demand to which it is subjected. Therefore, it is worth asking ourselves how much power we are using from our engine at any given moment, either out of mere curiosity or to know the "oversizing" of our steed.
To get an approximate idea, I propose the development of a simple formula based on physics that allows us to know, under certain circumstances, the power generated by the engine. Who is in? In the first place, we must delimit the experiment with the following starting hypotheses:
- The power developed to move the car at constant speed will be calculated.
- We consider a 30% of losses in the transmission
- The vehicle must overcome aerodynamic drag and rolling resistance.
- The wheels and the ground they tread on are considered to be non-deformable.

The power, measured in the International System in watts, is given by the relation P = F * v, where "F" is the force developed by the engine and "v" the speed of the vehicle. And how do we calculate the developed force? Very simple, thanks to a certain Isaac Newton, who, under the effects of unfermented and unpeeled cider, formulated his First Law:
"If the resultant of the forces acting on a body is zero, that body will remain at rest if it was previously at rest, and if it was in motion, it will perform a uniform rectilinear motion."
We have said that the vehicle is moving at constant speed, therefore, the force developed by the engine is exactly equal to the resistance it must overcome. The aerodynamic resistance is due to the movement of the vehicle through the fluid that surrounds it, and is calculated with the expression:
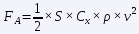
"where "S" is the front section of the vehicle, "Cx" is the aerodynamic penetration coefficient in the forward axis, "ρ" is the density of the fluid (in this case air) and "v" is the velocity. Rolling resistance is due to the contact between two bodies rolling without sliding, and is due to the elastic deformations suffered by both the tyre and the asphalt (yes, asphalt also deforms, there is no room for rigid solids here).
This resistance should not be confused with friction, which occurs when the body slides without rolling, for example, when the TV remote control slides across the table. The rolling resistance depends on the material of the wheel and the floor, a higher stiffness leads to a lower coefficient.
As a curiosity, the low rolling resistance is one of the reasons for the profitability of rail transport, with a coefficient (steel-steel) dozens of times lower than the rubber-asphalt coefficient, in exchange for some ceremonious starts, very long braking necessarily soft and crossing your fingers to face climbs (to help you have traction control and sand, which when deposited on the rail is nailed between it and the wheel, improving traction).
Simplifying a bit, the rolling resistance is calculated by:
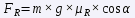
where "m" is the mass of the vehicle, "g" is the acceleration of gravity, "μR" is the rolling coefficient and "α" is the angle formed by the plane of the vehicle's motion with the horizontal. Once we know the values of the two forces FT = FA + FR, we would only have to go to the power formula and the miracle will have been worked. Let's calculate the power for some concrete cases, at a constant speed of 90 km/h.

Citröen Saxo 1.5 D
It is not the last cry, but as it is endearing to the undersigned, could not miss the appointment, plus it serves as a reference for any city car.
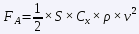
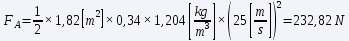
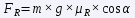
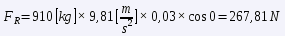
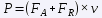
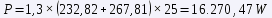
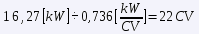

BMW 520d saloon (G30)
A tireless swallower, all E-segment vehicle has as its main feature its comfort for long trips, so it will be much of the time subjected to this type of driving.
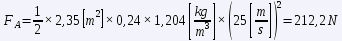
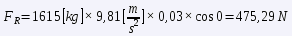
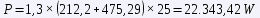
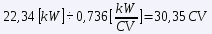
The results are very striking. In both cases it is striking that at 90 km/h, the aerodynamic drag is still lower than the rolling resistance, but it is worth noting that the former increases with the square of the speed, and the latter is practically constant. Looking at the numbers, the nice French car uses almost 39% of its power (57 hp) to maintain this cruise, while the brand new German car uses only 16% of its power (190 hp).
It is clear that physics rules, the only times when more horsepower is required is when acceleration is needed to reach the desired cruising speed. For the same acceleration value and set speed, the power is proportional to the mass and morphology of the car, hence the importance of losing mass in pursuit of consumption (the mass affects very little to flatten) and sculpt the shapes (to reduce consumption at high cruising speeds).
The power needed to drive at high speeds soars, aerodynamics becomes vital.
On the other hand, it is striking that the BMW has a lower aerodynamic drag than the Citröen, but its greater length helps to develop the shapes, plus the years do not pass in vain, and neither do the hours in the wind tunnel. Remember that the real values of power used should be higher than those obtained, due to the simplification made in the rolling resistance, the main intention is that you put the data of the car you want and you get an idea of its performance.
To do this, you have to go to the internet and find the following data:
- Frontal surface, in square meters
- Cx
- Mass in running order, in kg
Everything else remains unchanged, if you want to change the speed, don't forget to divide it by 3.6 to convert it to m/s, and if you want to know how much the motor works going up a slope, just change the zero that accompanies the cosine by the value of the angle you want.

Anyone fancy a comparison between a Ferrari F40 and a Mercedes-Benz Actros?