Maximum torque is the "ugly cousin" of power. Unknown to a large part of the population, misunderstood by others, it is an extremely important value, not only because of its specific amount at a given point, but also because of its variability throughout the revolutions at which the combustion engine can rotate.
Today we are going to focus on explaining, in extremely plain language, what the hell maximum torque is, where it comes from, how it is measured and what importance and relationship it has with respect to power.
We are going to focus our explanation on internal combustion engines with pistons, which are the most common on our roads, although much of the text is equally applicable to any other type of engine.
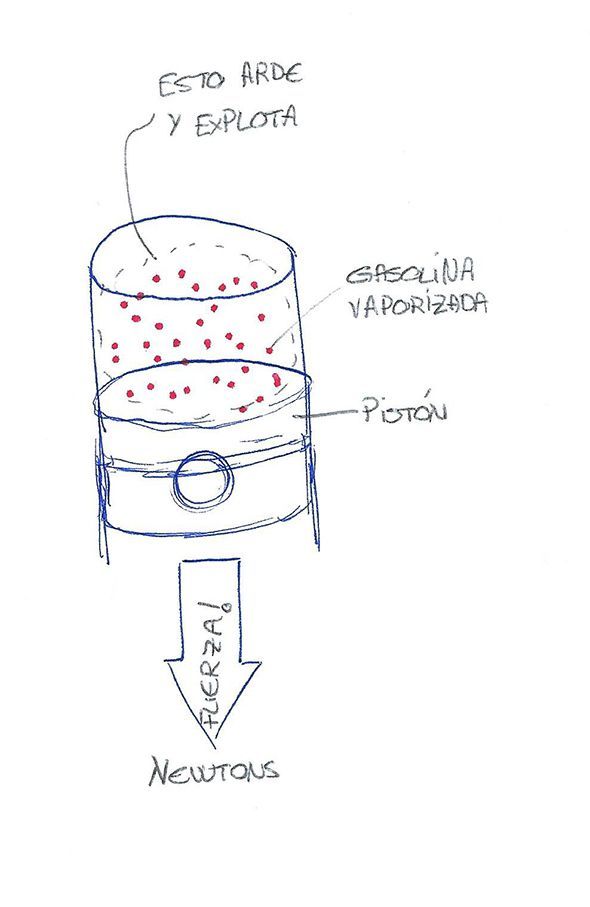
This piston, as you can imagine, is subjected on one side to the pressure generated by the explosion, so it tends to be thrown downwards at full speed. The energy of the explosion generates pressure on the face of the piston, and if you multiply that pressure by the surface area of the piston, you get a force.
That unit of force is easy to imagine, isn't it? In our International System of Measurement, that force is measured in newtons.
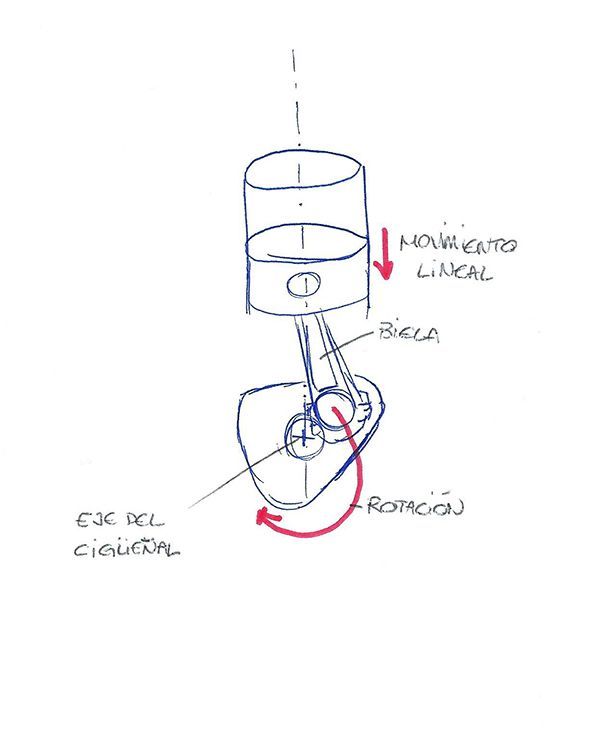
But of course, here we have a problem: The force is in a straight line, perpendicular to the plane formed by the surface of the piston, right? Linear movements, straight line forces, are of little use here to move a car, where what we need is to have a rotational movement to turn the wheels.
That's what the connecting rod and crankshaft are for. Anchored to the piston, they are responsible for transforming into 180 degrees of rotation all the way down the piston after the explosion, until the mixture of gasoline and air is finished burning. Taking advantage of the reciprocating mechanism, the other 180 degrees of rotation are used to return the piston to the top of the cylinder.
But here what interests us is to know what happens with the force of the explosion and how we can take advantage of those newtons to move our car.
The law of the lever
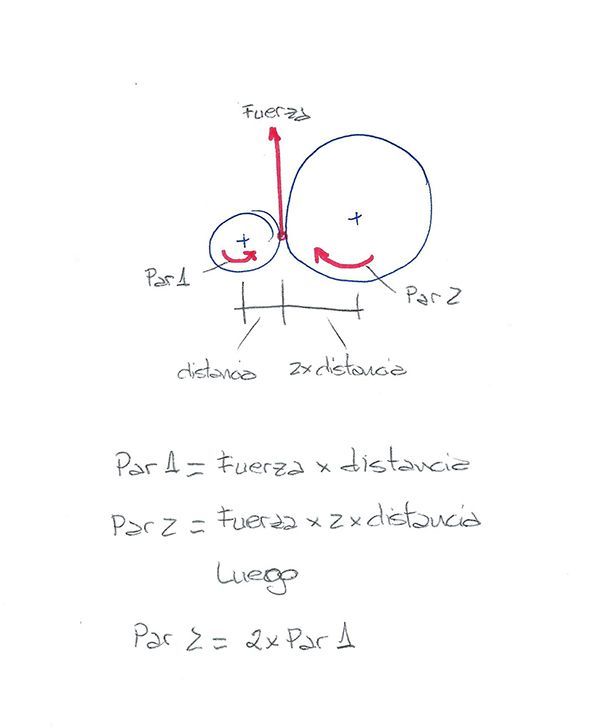
And this is where torque comes into play for the first time. For this we have to put another explanation in between the one we have at hand: The momentum of forces, or what is known as "the law of the lever".
If you remember, either because you have studied it or because you have experienced it, when you go to ride on a seesaw with a friend, if your friend is much fatter than you are, you have to position yourself closer to the axis of rotation of the seesaw so as not to send you into outer space when you drop your full weight on your seat.
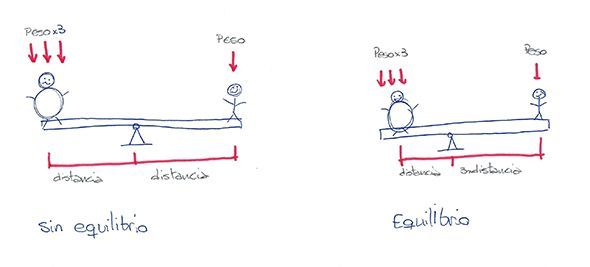
The idea is simple: A pair of forces is the combination of a force multiplied by a distance. In the case of the see-saw, the force is the force generated by the weight of the person, and the distance is the distance from our butt to the axis of the see-saw.
In the case of the seesaw what we want is to have balanced pairs of forces so that it moves slowly, so on both sides of the seesaw axis we want the multiplication of weight by distance to be identical. That's why it matters so much where we sit so as not to fly away...
The law of the lever, the torques, are present in all aspects of our common life: from a nutcracker to a nail clipper or a pair of scissors. And your car engine is no exception.
The big difference in any of these machines is that we are not interested in having two balanced pairs of forces, as in the seesaw, but we want to take advantage of having a force at a distance to generate work.
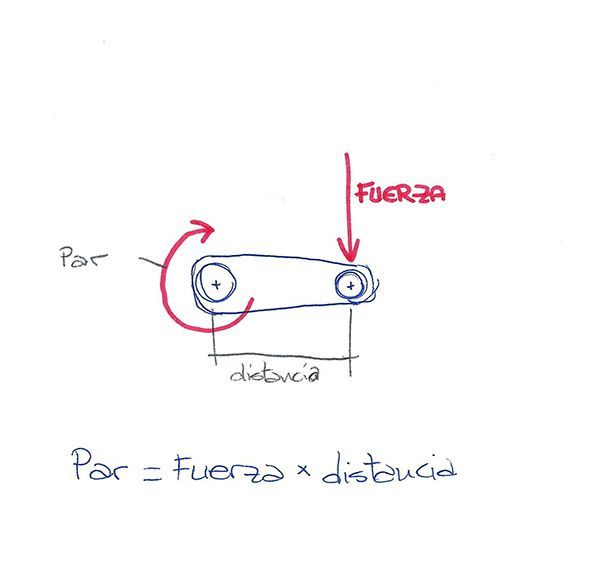
Now that you have the perception of "force over distance" as "torque", we can go back to the reciprocating combustion engine. When the force of the explosion takes full force at the head of the piston, it reaches the crankshaft almost in line. As the piston moves down, until it reaches 90 degrees of rotation, thanks to the connecting rod, the force is transferred further and further away from the crankshaft's axis of rotation, as you can see in the drawing.
Then, for the remaining 90 degrees until the piston reaches the bottom, the connecting rod gradually transfers the force back more and more in line with the crankshaft axis.
In addition to this, the pressure on the piston is not constant during the entire explosion and stroke of the piston, but decreases little by little, as the expansion of the burnt mixture takes place.
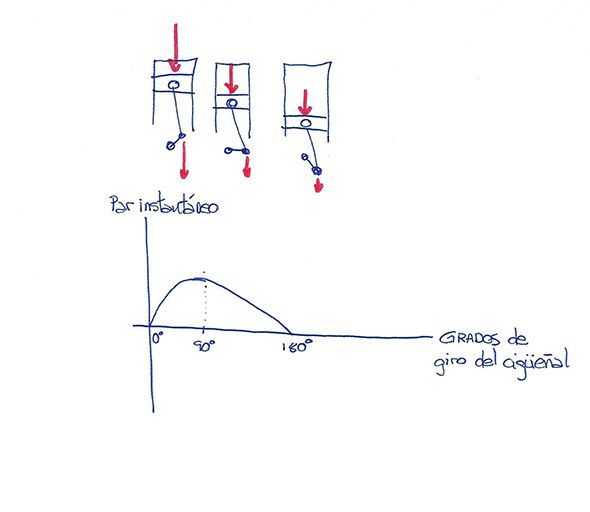
The important thing to remember here is that, as if it were a restless child, the force generated by the piston is transformed into a rotational "torque", in a variable way. That is to say, the force of the piston is multiplied by a distance that varies during the entire downward stroke of the piston. It is as if the child were moving in its rocker seat, from almost the axis of the rocker to the end.
What we have achieved with this reciprocating motion system is to have transformed a linear force created by the controlled combustion of gasoline into a "torque". The "torque" is what allows us to have "tucked" that force into rotational energy that we can transmit, increase, modify and use for many things.
Multiply by cylinders
By now it will have become clear to you that this "torque" is not a constant figure that is obtained in a simple way from combustion. It is a variable figure, which goes from almost zero at the first degree of crankshaft rotation, to its practical maximum when the crankshaft has turned 90 degrees, to fall back to almost zero for the rest of the half turn.
So, for every full turn of the crankshaft we have a "stroke" of force on the shaft, but other areas less powerful. Also, in four-stroke reciprocating engines only one out of every two revolutions produce explosion, so in total, for every 720 degrees of crankshaft rotation only 180 give us "work", while the rest are used to pump exhaust gases and the mixture and compress it before it can be burned. This is why a single cylinder engine is so vibrating and uninteresting, as it "kicks hard" in half a turn, and needs 3 more half turns before it kicks again.
Each kick is a vibration, and the rest of the crankshaft travel has to be done with some of the energy extracted from the engine in that combustion process.
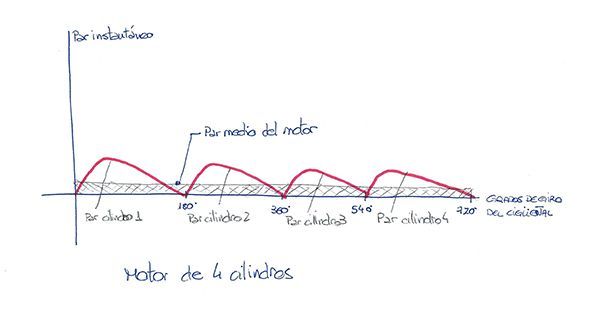
To smooth out these localized kicks, reduce vibrations and improve engine life, as well as the way torque is delivered to the wheels, since almost the beginning of the combustion engine times what is done is to mix several cylinders. The usual count is four cylinders. In this way the engine always has one of the four cylinders in the "torque" generation zone, while the other three use part of that torque to make one of the other three movements necessary for the process.
Ultimately this means that, more or less, every half turn of the crankshaft has the same "energetic pulsation" on the engine's rotation axis. Ultimately, torque is measured as an average figure. That is, it is the average that takes these pulsations into account to give a continuous approximate figure.
But be aware that the engine speed has an influence.
The problem doesn't end there. Ok, you have an "average" torque of "x's". Let's say for example 100 Nm. But that torque is far from constant.
The peculiar design of reciprocating engines makes the combustion process and the pressure extracted from it, and hence the force, very dependent on the speed at which things happen. Think about it, the time it takes for the gasoline/air mixture to burn is a more or less fixed factor. The more combustion you want to have per minute (more revs per minute, and more power and consumption), the faster you have to make that combustion factor happen.
This is where the compromise and problem that engine designers have been facing for over 100 years comes in. When designing the combustion chamber of an engine of this type, the designer has to try to make sure that it can work in a variable range of combustion speeds. An engine does not always work at the same revolutions. In fact, the main drawback of piston engines is exactly that: they do not offer the same torque throughout the rev range, due to these changes in combustion speed. Optimizing combustion at different speeds becomes a challenge.

Engines like the old Cosworth DFV for Formula 1 were meant to rev only at high revs all the time, with almost no torque at low revs.
If you design an engine to burn the mixture very fast, with large and generous intake and exhaust valves, up to a total of four, and a highly engineered combustion chamber geometry to make it easy for the flame to work once it starts, you will get an engine that will deliver a lot of torque, but only at high down piston speeds. In other words, it will be a very sharp engine, with a lot of torque at high revs, but with little torque at low revs.
If, on the other hand, you slow down the combustion process, work with an engine with a slow and progressive piston stroke, with a flame that burns little by little (relatively speaking), you will have an engine that is better able to offer torque at low revs, but which will ultimately perform poorly when you demand it to turn faster.
As a general rule, due to many factors derived from friction and combustion speed, it is usually more efficient to burn the mixture slowly than at high speed, but the speed of rotation influences the power, as we will explain below, so you can't waste that aspect either.
A constantly variable pair
The moral of the above is that the engine delivers a torque to the crankshaft that is continuously variable. To begin with, it varies constantly with each combustion, and to continue, the intensities of these pulses also vary depending on the rotational speed of the engine. So, constancy is not its thing.
That's why so much work has been done in recent times to try, by means of variable distribution, variable intake, direct injection, variable valve lift, variable supercharging and other technological remedies, with the idea of improving and filling out the torque curve of the engines, so that the combustion speed can be adapted to each engine speed, to keep the torque as uniform as possible, from idle to ignition cut-off.
But how is torque transmitted and multiplied to the wheels?
Well, it has already been made clear to us that torque is a rotational force, so to speak, which is variable in pulses. You have to get those pulses of energy to the wheels so that they act like little strides on the tires to pull the car forward, right?
To do that, from the crankshaft through the clutch, you get to the gearbox. And here comes the magic. The power of an engine cannot be multiplied with a magic gearbox. If the engine delivers 100 horsepower through its pistons, 100 horsepower will reach the wheels (less, due to the friction of the gearbox), never more.
But torque can be multiplied, how? By subtracting speed from the axle rotation. So, if we have 100 Nm of torque on the shaft of the engine turning at 2,000 RPM (210 radians per second), we can achieve 200 Nm on the shaft that is coupled to the wheels, by simply halving its revolutions per minute to 1,000 (105 radians per second).
How is this achieved? To explain it, imagine it in "little kicks" or pulses: Imagine that at the end of the engine shaft, at the crankshaft, we have a gear with 100 teeth. Each tooth makes a force, a kind of pulse or concrete kick that adds up over 2,000 revolutions. If we take and associate it with a gear that has twice as many teeth, 200, each tooth of the crankshaft gear will have to pass twice through the 200-tooth wheel for it to complete one revolution, correct? Since each tooth "pushes" or "kicks" the 200 tooth gear twice, you are multiplying the torque by two. Magic, right?
The problem is that you lose rotational speed, so what seems like magic also has a trade-off.
Eventually, after a few gears, those pulses or kicks that are generated at the crankshaft end up reaching the wheels multiplied, but also the rotational speed is reduced more and more, with each gear. In the end we have a rotational speed for the wheels, and they transmit those pulses to the asphalt.
It is the wheels that are responsible for converting the rotational energy of the axle to which they are associated (the bearing) into linear force that pushes the car through the contact between tire tread and asphalt.
The difficulty of constantly changing engine speed
As you can imagine, the big question here is to find out how much we want to reduce the rotational speed to achieve the necessary force on the wheels to move the car. What you do is create a very large torque multiplication for first gear, so that the car can start from 0 km/h and accelerate.
When it accelerates fast enough, the engine is also approaching its maximum rev limiter. That point at which combustion starts to be so fast that it is no longer effective. At that point you change gear. When changing gear to second, the torque of the engine is multiplied less times. In other words, the number of "kicks" per wheel rotation available is reduced. The torque to the wheels is therefore reduced. But as the wheels are spinning faster, although the kicks, the pulses they have per turn, are less intense, this is compensated with more turns every second.
And this is where the term power comes into play. Let me explain. Imagine you go out for a run, do you prefer to take a few very long and powerful strides, or do you prefer to take many more strides but much shorter and less powerful? Obviously this depends on how fast you are running. But this is the perfect simile for the combustion engine: When we go at low speed with a low gear, what we do is that the engine strides very hard (a lot of torque transmitted to the ground), but the amount of wheel spin against the asphalt (the speed) is low. As the car gains speed and puts higher gears, what happens is that the car begins to give less and less strong strides, but gives many more strides per minute (the wheel turns many more turns every second, as the car goes faster). All this until you reach that point of equilibrium where the amount and power of the strides is not able to accelerate the car more.
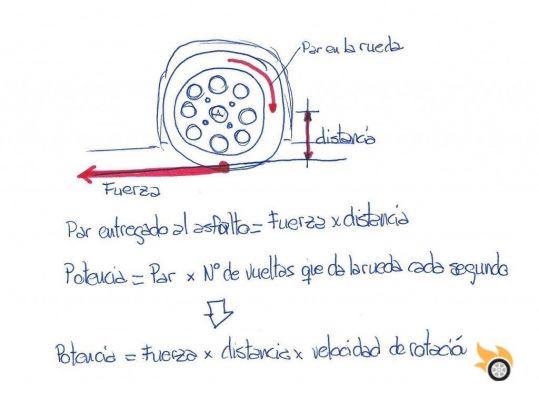
Well, there is a factor that directly relates these two values: Stride force, kick or pulse, and the number of times the wheel turns on the asphalt: Power.
Power is measured as the multiplication, the product, of the torque by the number of revolutions at which the axle is turning at that precise moment. The power is more or less constant in the engine, so the figure you get from multiplying the torque at the crankshaft by the speed at which the crankshaft is turning is practically the same as if you multiply the torque that the wheels are transmitting to the road by the speed at which they are turning (there is always a difference due to the friction generated in the gearbox and the transmission).
Power and torque are "two sides of the same coin", as they are inseparable. When a "smart ass" tells you in the bar that "torque is more important than power", he is wrong. The person who says the opposite, that power matters more than torque, is also wrong.
So which is more important, power or torque?
Like almost everything in this life, this question cannot be answered with a concrete answer. We live in a world obsessed with numbers. The maximum torque figure, the maximum power figure, the revs figure... but in reality, what really counts is "the whole": The complete torque curve on a graph, and the choice of gearbox associated with the car.
Let me explain: As I have already told you a thousand times above, the amount of torque is variable depending on the revs. The power curve is the simple multiplication of that amount of torque by the revolutions at which the engine delivers it at each point. In other words, when you measure the power curve you are measuring the torque curve and multiplying (or vice versa), as they are two completely inseparable factors.
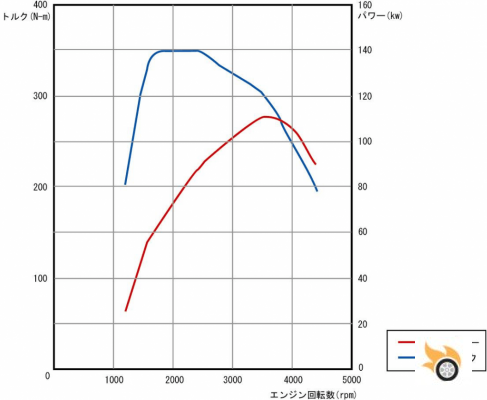
The blue line is the (official) torque curve of Subaru's boxer diesel engine (although it is clearly visually altered to show a completely flat area which in reality is not the case).
What really counts is "the shape of the torque curve", not its absolute values. As you can imagine by now, the ideal is an engine that is capable of delivering "many very intense pulses" over a large rev range, i.e. with a large variation of combustion speeds.
The best designed engine is one that is able to work well when we are at low revs, offering few very intense pulses, but that is also able to work well when we demand many pulses (many revs) with an adequate intensity.
This type of motor not only has a high torque figure, but also has a flat torque curve along the graph. In other words, the torque curve is "well filled", which is what we sometimes tell you in tests.
This, unfortunately, is not as common as it seems. And I'm going to explain with examples.
The classic naturally aspirated engine
The classic engines with two valves per cylinder and carburetion had the problem that their flexibility was very reduced: They only had a narrow margin where the combustion was tuned and produced efficiently. In other words, torque was achieved at a certain rpm.
Going out of that zone implied working with an inadequate fuel mixture, due to the carburation, to which was added the difficulty of the two-valve cylinder heads to work with large gas flows, which made them lazy. The moral of the story? They were very lazy at high revs, so they only worked well at low revs.
Because of this, to achieve speed, we had to use gearboxes with a lot of downshift, multiplying the torque a lot, and jumping gears to gain speed, but quickly hitting the engine's performance limit, which was reached especially early.
As the gearboxes were usually less than five ratios, the cars were particularly limited in their flexibility.
The atmospheric multivalve high-speed engine
The multi-valve cylinder head came along to solve this problem of sluggish engines at high revs. Putting in more valves allowed the mixture to burn faster when the engine was revving at high revs. That is, you could have more torque at high revs, by the simple addition of more combustion.
The big problem with these engines was that they were very bad at low revs. Having a combustion chamber designed to burn well when the combustion was fast, when the conditions demanded a slower burn, the engine did not get enough torque from the combustion.
Thus, the early four-valve-per-cylinder (and five-valve-per-cylinder) engines also faced a problem of poor flexibility, but centered at the top end of the rev counter.
But they had one fact in their favour, and that was that they gave more power than the two-valve-per-cylinder engines. Why? Because of simple basic arithmetic: If you can offer more torque at higher revs, as this is multiplied by the revs value to get the maximum power figure, ultimately you had more power.
But what was the point of having more power if it was all "up there"? As has been proven for decades since the introduction of four valves per cylinder, the trick was to play with the engine turning "high speed". If the gearbox was tight enough to allow you to drive all the time between 5,000 and 7,000 rpm (to say the least), you could take advantage of the extra power (the extra torque in that area of the rev counter multiplied by the rev speed), and go faster.
But in the real world, where drivers start and stop in traffic jams and between traffic lights, these engines had a lot of issues. Ultimately, design engineers had to resort to cylinder head designs that, while taking advantage of some of the four valves per cylinder to turn faster and go faster up top, were not fully optimized to work in that area of the rev counter, in order to conserve torque down low.
The engine with variable valve timing
Variable valve timing came in to solve part of that flexibility problem. The idea is to be able to have two engines in one: One that works well at low revs, with low combustion speeds, and another that works well at high combustion speeds. To do this, these engines play with the opening of the valves and the flow of gases and currents.
It is so complicated that another day we will investigate in a separate report, but for what we are explaining today we will suffice to say that this invention served to "fill" the torque curve. Let's say that what is achieved with the variable distribution is to add the torque curves of an engine with two valves per cylinder with the curve of a four valves per cylinder, which allows us to have a fuller torque curve, which as we mentioned above, is what ultimately is sought.
The modern supercharged direct injection engine
The epitome of all this is the modern turbocharged engines with direct injection and turbocharging. The idea behind current designs is to offer the maximum amount of torque possible for each engine speed, mixing all possible resources to have "a thousand engines in one engine".
By playing with variable valve timing, variable valve lift and supercharging, the engine can offer a lot of torque to the shaft when it turns slowly, but also be able to turn very fast without a noticeable loss of torque. In other words, "the ultimate in the ultimate". The ultimate flexible motor.
And that's why it's no good to compare or stick to data.
And it is this last type of engine that shows us the emptiness of the figures and of just being satisfied with the headlines. Although an engine from thirty or forty years ago could offer the same power and torque figures as a modern engine, when you sit down to drive it you quickly realise how different they are.
Where before we had engines that had a very localised power kick (in the maximum torque zone) and had to be used between that point and the rev cut-off point to get the best out of them, now we have engines that, far from working only in that zone "between kick and cut-off", are grateful and complete to use almost from idle to the end of the red zone. That is the great evolution, the great change not counted by the pure and hard figures, but that can be seen in the graphs.
It's true: We have lost "the kick", and with it, that "feeling" of "how this car runs". But we have gained strong engines, which run more than before, although sometimes it doesn't seem so or they don't transmit it.
The importance of gearboxes
The last big issue we are going to deal with here is the gearboxes. I told you above that it was another of the fundamental factors in this whole torque thing. After all, it is the gearbox that multiplies the torque and reduces the rotational speed of the axles in exchange.
The appearance of gearboxes with more and more ratios responds to this need to have the engine working in the smallest possible range of variation of revolutions per minute. Ideally, each gearbox should be associated precisely with the torque characteristics of each engine, so that the development of the gears allows us to always be in the good torque zone.
The problem is that, nowadays, with fuel consumption homologation regulations, instead of offering alternatives in the form of gearboxes optimised for the real world, manufacturers select the gear ratios to homologate the lowest possible fuel consumption.
Why? Well, because low fuel consumption sells cars, and in the end the customer demands "what sells in advertising". It is a disgrace that only the change of the NEDC fuel consumption approval procedure will be able to alleviate, if more realistic driving cycles are introduced, closer to the typical real use of cars.
Final moral
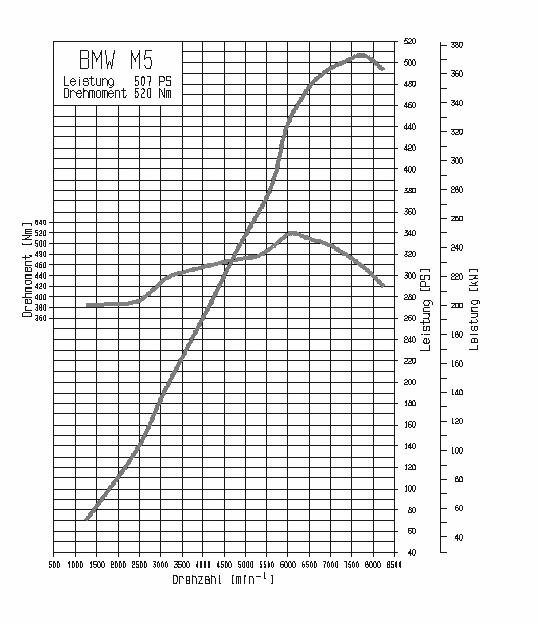
Actual torque curve of the V10 engine of the naturally aspirated BMW M5 of the last generation
I need a conclusion to close all this, and it is none other than "don't stick to the figures". There is no answer to the question "Is torque or power more important? It's the torque curve that counts. Just look at the graphs above and below this paragraph, where we compare the delivery of the last two BMW M5 engines.
At the end of the day, it's not the torque or power figure that is most important, it's the shape of the torque curve that tells us what the engine is like.
The upper one, which reflects the torque curve of the naturally aspirated M5 V10 shows us a sharp irregular torque curve that peaks at 6,000 rpm, leaving a fairly narrow margin of effective use of the engine. The counterpoint is the curve (visually altered in any case) that you have bjao paragraph, that of the V8 biturbo of the current M5, which has much more torque for much more time of the curve, showing a much more "full" engine, flexible, usable, and ultimately, quick to accelerate in any gear and circumstances.
Torque curve of the current supercharged V8 engine of the BMW M5
In a single sentence: The fuller, more constant and elongated the torque curve along the rev graph, the better for you.
Article originally published in May 2014, retrieved for Pistonudos.